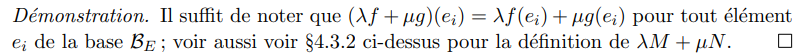À une matrice réelle \(M\in\operatorname{Mat}_{m\times n}(\Bbb R)\), on peut associer l'application linéaire \(f_M\)$$où \(\dot X\) est {la matrice de \(\operatornameMat_n\times1(\Bbb R)\) obtenue tout simplement en prenant les coordonnées du vecteur \(X\in\Bbb R^n\)
Définition :
Si \(f(e_i)=a_{1i}f_1+a_{2i}f_2+\ldots+a_{mi}f_m\) pour \(1\leqslant i\leqslant n\), on appelle matrice de \(f\) dans les bases \(\mathcal B_E\) et \(\mathcal B_F\) la matrice suivante : $$M=\begin{pmatrix}a_{11}&a_{12}&\ldots&a_{1n}\\ a_{21}&a_{22}&\ldots&a_{2n}\\ \ldots&\ldots&\ldots&\ldots\\ a_{m1}&a_{m2}&\ldots&a_{mn} \end{pmatrix}$$
Lorsque \(E=F\) et \(\mathcal B_E=\mathcal B_F\), on parle de matrice de \(f\) dans la base \(\mathcal B_E\)
Elle est composée de plusieurs colonnes, qui représentent chacune les coordonnées, dans la base de l'espace d'arrivée, de l'image d'un élément de la base de l'espace de départ
(Base, Coordonnées)
Application linéaire associée à une matrice
Produit de matrices d’applications linéaires
Matrice inverse d’une matrice d’application linéaire
Soient \(f,g\in\mathcal L(E,F)\) et \(M,N\) leur matrices respectives dans les bases \(\mathcal B_E\) et \(\mathcal B_F\)
Pour tout \((\lambda,\mu)\in\Bbb R^2\), la matrice de \(\lambda f+\mu g\in\mathcal L(E,F)\) dans les bases \(\mathcal B_E\) et \(\mathcal B_F\) vaut \(\lambda M+\mu N\)
(Combinaison linéaire)
Démonstration :